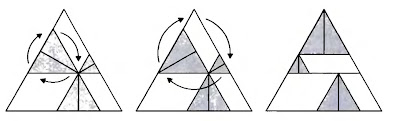
Sum of Squares
$1+2^2+3^2+\cdots+n^2 = \frac{1}{3}n(n+1)\left(n+\frac{1}{2}\right)=\frac{n(n+1)(2n+1)}{6}$
This originally came in Mathematics Magazine (1984 edition). The author of this ingenious proof is Prof. Siu Man Keung. This link provides further information regarding the article.
Comments
Post a Comment