Basel's Problem

$$1+\frac{1}{4}+\frac{1}{9}+\cdots = \sum_{n=1}^{\infty}\frac{1}{n^2}=\frac{\pi ^2}{6}$$



Now you might be thinking - "How on earth are they even related!!"

Well the reasoning is a bit too long to write it all out in this one post.
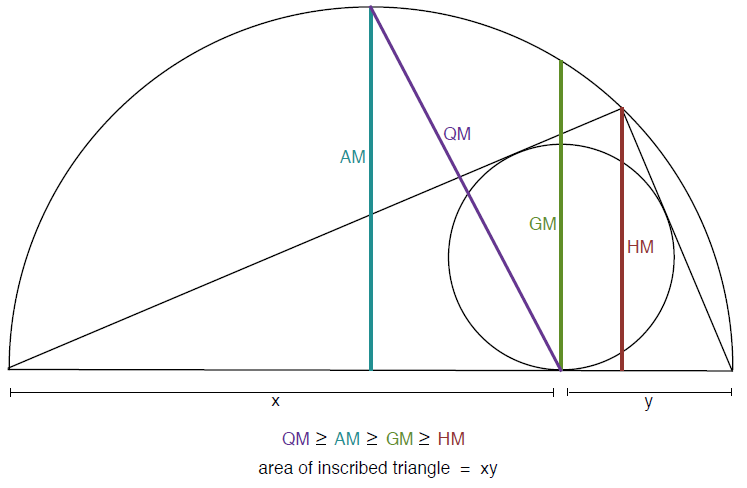
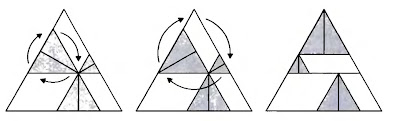
I suggest you have a look at this brilliant article by Mikael Passare -How to Compute $\sum_{n=1}^{\infty}\frac{1}{n^2}$ by Solving Triangles 

Comments

Post a Comment

Popular posts from this blog

Viviani's Theorem

Image
Viviani's Theorem states that for any point $\mathcal{P}$ inside an equilateral triangle $\mathcal{ABC}$ the sum of the lengths of perpendiculars drawn from P on the sides is equal to the length of the altitude.    Draw equilateral triangles from that point onto the sides of the triangle such that these 3 perpendiculars are the altitudes of the equialteral triangles.Now rotate the triangles as shown.Now it can be easily seen that the sum of the 3 perpendiculars=perpendicular of the  $\Delta ABC$  
Keep reading

Fibonacci Sum of Squares

Image
One can easily see that the length and breadth of the above rectangle are $\mathcal{F_{n+1}}$and $\mathcal{F_{n}}$. Area of the rectangle = $\sum$ Area of the squares or,$$\mathcal{F_{n}F_{n+1}=F_{0}^{2}+F_{1}^{2}+\cdots+F_{n}^{2}}$$
Keep reading