The Sierpinski Triangle

What is the Sierpinski Triangle?

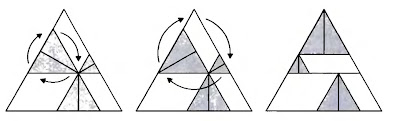
Let's consider an equilateral triangle.

Now remove the equilateral triangle joining the mid-points of the sides of the triangle.

Notice that the area of the new figure is $\frac{3}{4}^{\text{th}}$ the initial area. Now lets apply the same procedure to the 3 smaller triangles.


The following animation shows the development of the figure. 


Notice how the red triangle transforms to nothingness. As we repeat the experiment for an arbitrarily large number of times the net area of the figure becomes infinitesimally small. This fractal is referred to as the Sierpinski Triangle.

Enough writing!! Let's move on to what the blog originally was meant to be - proofs without words.

$$1+\frac{3}{4}+\frac{9}{16}+\cdots = 4$$

If you're having troubles figuring out why think about the net area being removed from the initial triangle.

Image Sources: Jim Milner Sculpture - Check it out. There are more demonstrations of such fractals.

Comments

Post a Comment

Popular posts from this blog

Viviani's Theorem

Image
Viviani's Theorem states that for any point $\mathcal{P}$ inside an equilateral triangle $\mathcal{ABC}$ the sum of the lengths of perpendiculars drawn from P on the sides is equal to the length of the altitude.    Draw equilateral triangles from that point onto the sides of the triangle such that these 3 perpendiculars are the altitudes of the equialteral triangles.Now rotate the triangles as shown.Now it can be easily seen that the sum of the 3 perpendiculars=perpendicular of the  $\Delta ABC$  
Keep reading

Fibonacci Sum of Squares

Image
One can easily see that the length and breadth of the above rectangle are $\mathcal{F_{n+1}}$and $\mathcal{F_{n}}$. Area of the rectangle = $\sum$ Area of the squares or,$$\mathcal{F_{n}F_{n+1}=F_{0}^{2}+F_{1}^{2}+\cdots+F_{n}^{2}}$$
Keep reading