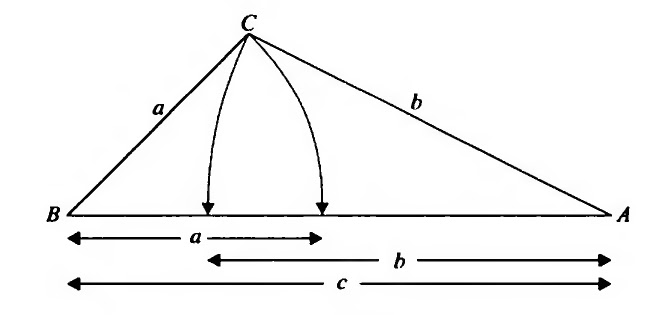
The Triangle Inequality

Without loss of generality we may assume $a\leq b\leq c$.
It is quite obvious that $$a+c\geq b\qquad a+b>c$$
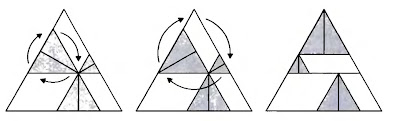
Rotate $\mathcal{BC}$ about $\mathcal{B}$ and $\mathcal{AC}$ about $\mathcal{A}$.

Now as we can see in the above diagram $$a+b>c$$

NOTE:$a+b=c$ would imply that the triangle is degenerate.

Comments

Post a Comment

Popular posts from this blog

Sum of odd numbers

Image
Proof of $$1+3+5+\cdots = n^{2}$$ Count the number of balls in the L shaped regions.Notice that they are odd numbers. Furthermore,count the number of balls considering the length or the breadth(they will turn out to be the same). Sum of all balls = (number of balls on the length)$^{2}$.
Keep reading

Viviani's Theorem

Image
Viviani's Theorem states that for any point $\mathcal{P}$ inside an equilateral triangle $\mathcal{ABC}$ the sum of the lengths of perpendiculars drawn from P on the sides is equal to the length of the altitude.    Draw equilateral triangles from that point onto the sides of the triangle such that these 3 perpendiculars are the altitudes of the equialteral triangles.Now rotate the triangles as shown.Now it can be easily seen that the sum of the 3 perpendiculars=perpendicular of the  $\Delta ABC$  
Keep reading