Basel's Problem
$$1+\frac{1}{4}+\frac{1}{9}+\cdots = \sum_{n=1}^{\infty}\frac{1}{n^2}=\frac{\pi ^2}{6}$$
Posts
Area of the Circle - Alternative
Here's an elementary way to find the area of a circle although I'm sure many of you are already familiar with it. Slice up the circle into 4 parts and stack them up as follows.
The Sierpinski Triangle
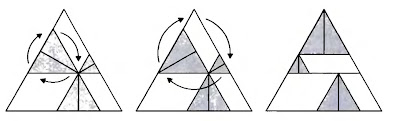
What is the Sierpinski Triangle? Let's consider an equilateral triangle. Now remove the equilateral triangle joining the mid-points of the sides of the triangle. Notice that the area of the new figure is $\frac{3}{4}^{\text{th}}$ the initial area. Now lets apply the same procedure to the 3 smaller triangles.
Sum of Squares
$1+2^2+3^2+\cdots+n^2 = \frac{1}{3}n(n+1)\left(n+\frac{1}{2}\right)=\frac{n(n+1)(2n+1)}{6}$ This originally came in Mathematics Magazine (1984 edition). The author of this ingenious proof is Prof. Siu Man Keung. This link provides further information regarding the article.
Integration by parts
Anyone familiar with calculus would know how useful this formula is at times when we are desparate.Here's an amazing proof: Source: http://www.math.ufl.edu/~mathguy/year/S10/int_by_parts.pdf
Viviani's Theorem
Viviani's Theorem states that for any point $\mathcal{P}$ inside an equilateral triangle $\mathcal{ABC}$ the sum of the lengths of perpendiculars drawn from P on the sides is equal to the length of the altitude. Draw equilateral triangles from that point onto the sides of the triangle such that these 3 perpendiculars are the altitudes of the equialteral triangles.Now rotate the triangles as shown.Now it can be easily seen that the sum of the 3 perpendiculars=perpendicular of the $\Delta ABC$